Soil salinity is one of the most serious agricultural problems. The cause of this process is the accumulation of salts in soil capillaries leading to a sharp decrease in plant fertility. Salt concentration left in plant capillaries, with insufficient amount of nourishing substances leads to plants dying.
Magnetic systems developed by Omni make it is possible to use traditionally unsuitable salty water (salt content of 410L/G) efficiently for irrigating crops. Obviously, when you irrigate with salty water, you subsequently increase the level of soil salinity which interferes with plant nutrient absorption. After magnetic treatment of water, there is a change of the physiochemical characteristics of water leading to improved filtration and dissolvability e.g. plant capillaries start to let either salt crystals or crystals of different chemical elements and suspensions pass. Magnetically treated water washed 3-4 times more salts out of the soil than non-magnetized water and at the same time oxygen concentrations increased by 10%.
Soil salinity affects vast areas of farming land and the area of salt-effected land is increasing rapidly. For example, approximately 32 million hectares of Australia's arable land have been rendered useless by salt. The cost in lost agricultural production is estimated at $3.5 billion per year.
After years of preparation, the Commonwealth Government released The Basin Salinity Management Strategy in 2001. This is an important co-operative approach between the Federal Government and the Governments of New South Wales, Victoria, South Australia, Queensland and the ACT to attempt to halt the spread of salt and in time to reduce salinity in the Murray-Darling Basin.
"The Murray-Darling Basin is the food bowl of the nation and is a major contributor to Australia's important and burgeoning food export markets. The Basin is home to unique and environmentally significant natural features, many of which are subject to international treaties. Over two million people directly depend on the natural resources of the Basin for their livelihood, and their future prosperity is dependent upon its sustainable management. These values are at risk from salinity."
(Basin Salinity Management Strategy, Annual Implementation Report, April 2003, p.3)
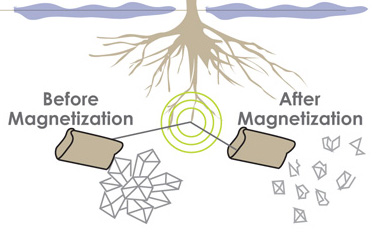
Removing salt from soil through magnetized water flushing
Salt in soil can only be removed by flushing with water. Magnetized Water applied to salty soil breaks down the salt crystals twice as fast as un-magnatized water allowing the salt to be leached from the soil. The process is lengthy and there is a cost but the cost of not beating this problem is infinitely greater.
Replacement of the natural ecosystems with conventional agriculture has resulted in large-scale disruption of the natural water cycle with severe environmental, economic and social consequences. Key natural resource management issues facing modern agriculture are: Soil and Water Quality, Soil Salinity, and Degradation of Riverine Ecosystems.
One of the greatest challenges facing Australia and the rest of the world is how to manage natural resources for a healthy future, while much of the landscape has critical salinity and water quality problems:
-
At least 2.5 million hectares (ha.) (5% of cultivated land) is currently affected by dry land salinity - this could rise to 12 million ha. (22%) at the current rate of increase.
-
At least 250,000 hectares of irrigated land (>10% of irrigated land) are presently salt affected out of a total of 2.3 million ha. of irrigated land. There is a potential for serious effects in a further 615,000 ha. over the next 20 years.
One third of Australian rivers are in extremely poor condition - within 20 years Adelaide's drinking water will fail World Health Organization salinity standards in 2 days out of 5 if no improvement is effected.
Land and water degradation, excluding weeds and pests, is estimated to cost up to $3.5 billion per year. (In addition dry land salinity has adversely affected biodiversity, e.g. the CSIRO estimates a resultant reduction in bird species of 50% in agricultural areas.
Infrastructure (buildings, roads, etc.) is being severely damaged in many rural urban centers.
Solutions to the salinity threat will largely depend on reassigning land and water use for the future and the taking of corrective measures, such as reclamation strategies for both dry land and irrigated or degraded lands affected by saline, saline-alkaline and sodic soils.
Causes of saline and/or sodic soils
Saline and/or sodic soil is caused by four separate conditions:
-
High salt in the parent material and low rainfall (low leaching),
-
High rainfall with poor internal drainage,
-
High water table that carries salt to the soil surface, and
-
High amount of salt being applied through chemicals, manure and poor quality irrigation water.
Before a reclamation system can be established, the factors causing salt accumulation must be eliminated.
Ions most commonly associated with soil salinity include the anions: chloride (Cl-), sulphate (SO4=), carbonate (HCO3-), and sometimes nitrate (NO3-) and the cations: sodium (Na+), calcium(Ca++), magnesium (Mg++), and sometimes potassium (K+). Salts of these ions occur in highly variable concentrations and proportions.
Effect of salinity on crop production
Plant growth and yield are limited mainly by the soil environment factors. Soil, water, nutrients, salinity, sodicity, structure, temperature, pH, and mineral toxicities can all interact to limit plant growth. In Saline soils although pH (<8.5) and ESP (<15%) are not high, CEC is >4 mmhos/cm and an excess of soluble salt in the subsoil restricts water uptake by crops; in the case of alkalinity there are Nutrient deficiencies (either because of a lack of nutrients, or because roots are unable to access them). The best way of understanding these limitations is to consider them in terms of the interacting factors that directly influence crop growth.
Traditional methods of reclamation of saline and sodic soils
Drainage carries the salts down through the soil profile and out of the rooting zone. Without drainage, salts will accumulate regardless of any applied soil amendments. However, implementing proper drainage systems is limited by expense and complex technical details.
Leaching and reclaiming saline soils
Saline soils cannot be reclaimed by any chemicals, conditioner, or fertilizer. Reclamation of these soils consists of simply applying enough high-quality water to leach the soil thoroughly. The water applied should be low in sodium but can be fairly saline (1,500 to 2,000 ppm total salt), as this helps to keep the soil permeable during the leaching process. Generally, about 12 inches of water are required to remove 70 to 80 % of the salt for each foot of soil. This is also a limited technique in that application of excess water can create extra management problems due to the threat of high water tables, increased expense of irrigation water and difficulty in maintaining adequate levels of soil nitrate for crop growth.
Reclaiming saline and sodic soils
In sodic soils, the exchangeable sodium is sometimes so great that the resulting dispersed soil is almost impervious to water. Sodic soil can be treated by replacing the absorbed sodium with a soluble source of cation i.e. calcium. Calcium may be made available through manipulation with native gypsum already in the soil, calcium in irrigation water (Calcium chloride), or commercial amendments. They may be useful where soil permeability is low due to low salinity, excess sodium, or high carbonate/bicarbonate in the water.
In order to reclaim soil to a depth of one foot, gypsum recommendations are as follows: tons of gypsum per acre = 1.7 X (meq Na/100 g - (CEC X 5%).
Reclamation of a foot depth of sodic soil on one acre requires approximately 1.7 tons of pure gypsum for each milliequivalent of exchangeable sodium present per 100 grams of soil. For example, if soil has a CEC of 20 milliequivalents per 100 grams and 30 percent exchangeable sodium, there would be 6 milliequivalents of sodium per 100 grams of soil. Thus, 10.2 tons of gypsum (6 x 1.7) per acre would be required to reclaim this soil.
If sodic soils contain no source of calcium (gypsum or free carbonates), then gypsum or a soluble calcium source needs to be applied. However, the reclamation process is not complete until most of the sodium is removed from the soil to at least a depth of three to five feet. Even then, more time is required for restoration of good soil productivity. This process is limited in that once the soil structure is completely destroyed, it is slow to return to a desirable condition. Correcting saline and sodic soils requires salt to be leached out of the soil profile. This requires good quality water, good soil permeability and good drainage. Amendments that supply soluble calcium are needed in huge quantity to correct sodic soils.
Reduce Soil Salinity Magnetized Water Technology
For over 30 years scientists researched the effects of magnetic fields on plants and a method of magneto-hydro dynamical activisation of irrigation waters. From this research exciting new applications have been developed and tested in Europe, Middle East and Australia. The applications include physical- chemical changes of irrigation water parameters, resulting in improvement of filtration properties and in an increase in the dissolving properties of water.
Research shows that these changes result in an increased ability of soil to get rid of salts and results in a better assimilation of nutrients and fertilizer in plants during the vegetation period. Plants irrigated with magnetized water easily take up mineral salts from the soil and no sediment is formed on the soil surface.
The advantages of using magnetic water for irrigating crops are as follows:
-
Vegetation period decreases by 15-20 days, therefore the crops ripe 15-20 days earlier than normal
-
Crop production increases from 15% to 100%
-
Plant disease rates dramatically decrease
-
The taste of agricultural products improves
The photographs below show results from an experiment that included using salt water for irrigation of different plants. In each case, the salt content of the water was 10000 PPM. The results shown on the left are those where magnetized water was used with seeds that had undergone magnetic treatment. The results on the right are those from the control group where non-magnetized water and untreated seeds were used.



